Как известно, мы живем в трехмерном мире. В нем, соответственно присутствуют три координаты — длина, ширина и высота. Все к этому приспособлены и мало кто думал о том, как бы мы воспринимали мир, если бы координат было меньше или больше. Об этом и будет эта статья.
Итак, начнем с азов. Нульмерное пространство нам сложно представить, учитывая то, что в нем нет ни одного измерения. Представить его можно точкой и ничем более.

Нульмерный куб
Одномерное пространство уже представить намного легче, так как здесь можно провести линию. Но повернуть, развернуть ее невозможно, даже посмотреть с другой стороны, так как координата всего одна.

Одномерный куб
С двумерным пространством знакомы многие. Раньше даже игры делались двумерными. Есть два измерения — высота и длина, либо же, если вид сверху, длина и ширина. В нем, конечно же, ориентироваться намного легче.
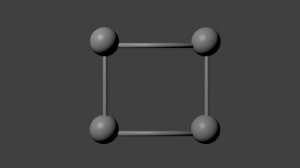
Двумерный куб (квадрат)
В трехмерном пространстве мы живем, о нем рассказывать нечего. Но видим мы его двумерным, если быть точнее его двумерную проекцию на нашу сетчатку глаза. Многие могут подумать, что это ложь, но для них есть железный аргумент: постарайтесь посмотреть на обратную сторону объекта, оставаясь на месте. Если у Вас это вышло, вероятнее всего, вы и вправду обладаете трехмерным зрением либо же обманываете. Именно это и называется трехмерным зрением, способность видеть все: обратную сторону объекта, человека насквозь, внутренности компьютера и так далее.
Доказать данный факт так же просто: представьте кота в двумерном мире: если вы видите его шерсть и морду, вы представили его неправильно, ведь в этом пространстве нету третьей координаты, это значит, что любой трехмерный объект, представленный в двумерном виде, автоматически становится плоским. Кот в такой вселенной просто погибнет, останется только его оболочка. Сделать кота живым в таком пространстве можно только представив все его органы поверх всего.
С трехмерным пространством все соответственно. Большинство людей говорит, что у нас трехмерное зрение и его придает нам два глаза — ложь. Такое зрение называют бинокулярным, оно позволяет выяснить примерное расстояние и глубину объекта.
Теперь перейдем к четырехмерному пространству. Множеству людей представить его является сложным, но можно дойти до его представления логическим путем.
Итак, построим нульмерный куб.
Теперь скопируем его, вставим рядом с ним и соединим. Это — одномерный куб.
Так же скопировав одномерный куб, сопоставив его рядом и соединив выходит уже двумерный куб. Думаю, суть понятна.
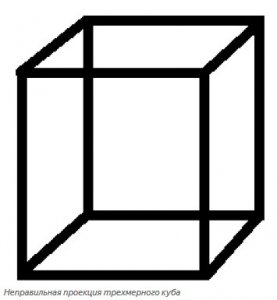
Проделав те же действия, мы получаем трехмерный куб. Но данное представление в корне неверно, ведь мы видим куб таким, каким он представлен на картинке ниже - все дело в перспективе. В четырехмерном пространстве также есть перспектива, но она сильно отличается от нашей.
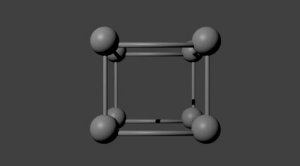
Сделав то же самое, что и с трехмерным кубом, мы получаем двумерную проекцию трехмерной проекции четырехмерного гиперкуба. Сложно представить, что это реально куб, но, будучи мы в четырехмерном пространстве, сомнений бы не возникло.

двумерная проекция трехмерной проекции четырехмерного гиперкуба (неверная)

двумерная проекция трехмерной проекции четырехмерного гиперкуба (правильная)
Вращение такого куба выглядит следующим образом:
Нам сложно понять, как это можно назвать вращением, ведь это деформация. Но деформация лишь для нас, для жителей четырехмерного мира все будет выглядеть очевидно.
Четвертое измерение можно представить, посмотрев на геймплей игры, которая основана на этом:
Четырехмерное пространство выражено на трехмерную проекцию, поэтому смена координаты выглядит настолько необычно. Еще один способ понять — это вращение обыкновенного куба. Постарайтесь посмотреть на это, забыв о перспективе — обычная деформация граней — по совместительству дополнительное доказательство нашего двумерного зрения.
Итак, начнем с азов. Нульмерное пространство нам сложно представить, учитывая то, что в нем нет ни одного измерения. Представить его можно точкой и ничем более.

Нульмерный куб
Одномерное пространство уже представить намного легче, так как здесь можно провести линию. Но повернуть, развернуть ее невозможно, даже посмотреть с другой стороны, так как координата всего одна.

Одномерный куб
С двумерным пространством знакомы многие. Раньше даже игры делались двумерными. Есть два измерения — высота и длина, либо же, если вид сверху, длина и ширина. В нем, конечно же, ориентироваться намного легче.

Двумерный куб (квадрат)
В трехмерном пространстве мы живем, о нем рассказывать нечего. Но видим мы его двумерным, если быть точнее его двумерную проекцию на нашу сетчатку глаза. Многие могут подумать, что это ложь, но для них есть железный аргумент: постарайтесь посмотреть на обратную сторону объекта, оставаясь на месте. Если у Вас это вышло, вероятнее всего, вы и вправду обладаете трехмерным зрением либо же обманываете. Именно это и называется трехмерным зрением, способность видеть все: обратную сторону объекта, человека насквозь, внутренности компьютера и так далее.


Доказать данный факт так же просто: представьте кота в двумерном мире: если вы видите его шерсть и морду, вы представили его неправильно, ведь в этом пространстве нету третьей координаты, это значит, что любой трехмерный объект, представленный в двумерном виде, автоматически становится плоским. Кот в такой вселенной просто погибнет, останется только его оболочка. Сделать кота живым в таком пространстве можно только представив все его органы поверх всего.
С трехмерным пространством все соответственно. Большинство людей говорит, что у нас трехмерное зрение и его придает нам два глаза — ложь. Такое зрение называют бинокулярным, оно позволяет выяснить примерное расстояние и глубину объекта.
Теперь перейдем к четырехмерному пространству. Множеству людей представить его является сложным, но можно дойти до его представления логическим путем.
Итак, построим нульмерный куб.
Теперь скопируем его, вставим рядом с ним и соединим. Это — одномерный куб.
Так же скопировав одномерный куб, сопоставив его рядом и соединив выходит уже двумерный куб. Думаю, суть понятна.
Проделав те же действия, мы получаем трехмерный куб. Но данное представление в корне неверно, ведь мы видим куб таким, каким он представлен на картинке ниже - все дело в перспективе. В четырехмерном пространстве также есть перспектива, но она сильно отличается от нашей.
Сделав то же самое, что и с трехмерным кубом, мы получаем двумерную проекцию трехмерной проекции четырехмерного гиперкуба. Сложно представить, что это реально куб, но, будучи мы в четырехмерном пространстве, сомнений бы не возникло.

двумерная проекция трехмерной проекции четырехмерного гиперкуба (неверная)

двумерная проекция трехмерной проекции четырехмерного гиперкуба (правильная)
Вращение такого куба выглядит следующим образом:
Нам сложно понять, как это можно назвать вращением, ведь это деформация. Но деформация лишь для нас, для жителей четырехмерного мира все будет выглядеть очевидно.
Четвертое измерение можно представить, посмотрев на геймплей игры, которая основана на этом:
Четырехмерное пространство выражено на трехмерную проекцию, поэтому смена координаты выглядит настолько необычно. Еще один способ понять — это вращение обыкновенного куба. Постарайтесь посмотреть на это, забыв о перспективе — обычная деформация граней — по совместительству дополнительное доказательство нашего двумерного зрения.
Для просмотра ссылки необходимо нажать
Вход или Регистрация